Project Notes

This was my Master's thesis in Engineering Technology: Electronics-ICT at KU Leuven.

Supervisor: Prof. Greet Vanden Berghe

Summary:

Developed a novel ruin-and-recreate local search operator (SMRI) that strategically deconstructs and rebuilds schedules by Selecting tools, Matching jobs through tool-based clustering, Removing them strategically, and reinserting with a greedy best-Insert strategy. Designed custom data structures, optimized KTNS decoder and implemented delta evaluation techniques, for efficient search. Achieved optimal results on all small benchmark instances and within 2-8% of state-of-the-art on large instances with competitive or better runtime.

Technical Deep Dive: The Paper

The next sections represent the formal paper derived from this research. It is a focused, technical deep dive.

• For a quick technical read: You can read the paper text directly below or Download the Paper (PDF).

• For the full perspective: I recommend downloading the Complete Thesis (PDF). The thesis includes extensive work not found in the paper. Such as an extensive literature study, comments alongside the improved ktns decoder and a comprehensive explanation of the problem and how local search is applied to it. Please note that the thesis is written in Dutch.

Abstract

Using tools for an extended amount of time without repeated switching is an efficient way to execute tasks or jobs. The Job Sequencing and Tool Switching Problem wants to take advantage of this fact. Frequently machines are capable of handling various jobs that each require their own set of tools. It is not conceivable to store these all at once. Hence switching is required; a time-consuming process. However, it is possible to significantly lower these switching times. By precisely arranging jobs and accommodating tools that are required later. Utilizing a heuristic approach it is possible to solve problems that would otherwise be impracticable to solve. This work introduces an elegant Ruin and Recreate method that allows for the exploration of a broad neighborhood while keeping tabs on the relationships between jobs. A significant speedup in the decoder and local Search procedure is achieved by using unique problem properties. Allowing a wide range of solutions to be explored in an acceptable time. Finally, choosing an appropriate objective function avoids plateaus in the search landscape.

Introduction

Frequently machines are capable of handling various jobs that each require their own set of tools. An example would be machining a part to a precise shape using different drills. Tools can be kept inside of a magazine, this way the machine can complete jobs without stopping.

Unfortunately, there is often not enough capacity for all tools of all jobs. Thus, switching is required when transitioning. A considerable amount of time could be wasted, tools may have to be calibrated or could be very heavy.

Choosing a good job sequence may therefore prove beneficial. Moreover, if sufficient capacity is left in the magazine tools could simply be kept in the magazine for later jobs. The goal of this paper is to develop a solution in order to minimize these switches as much as possible.

Problem Overview

Known as the "Job Sequencing and Tool Switching Problem" it can be stated formally in the following way: Given a set of N jobs each requiring a specific set of M tools and a magazine with a certain tool capacity $C$. Determine the order each job is carried out in and which tools are needed during that job, in order to minimize the number of tool switches needed.

Many variations and applications exist. Parallel jobs ¹, Tool dependent switching cost ² …. Although these variations are interesting, the focus here is on the uniform variant: Tools are uniform in size and can be put anywhere in the magazine, switching time is constant, one machine is used and all tools of one job can fit in the magazine at once..

Formulation

Let $J=\{1,2,...,N\}$ be the set of jobs, $T=\{1,2,...,M\}$ the set of all tools and $T_j$ the set of tools required for a job where $j \in J, T_j \subseteq T$. The magazine size is $C$ and $C \leq max(|T_j|) , j \in J$³.

SSP instance example 1Example from Paiva Et. al [^Paiva2017]

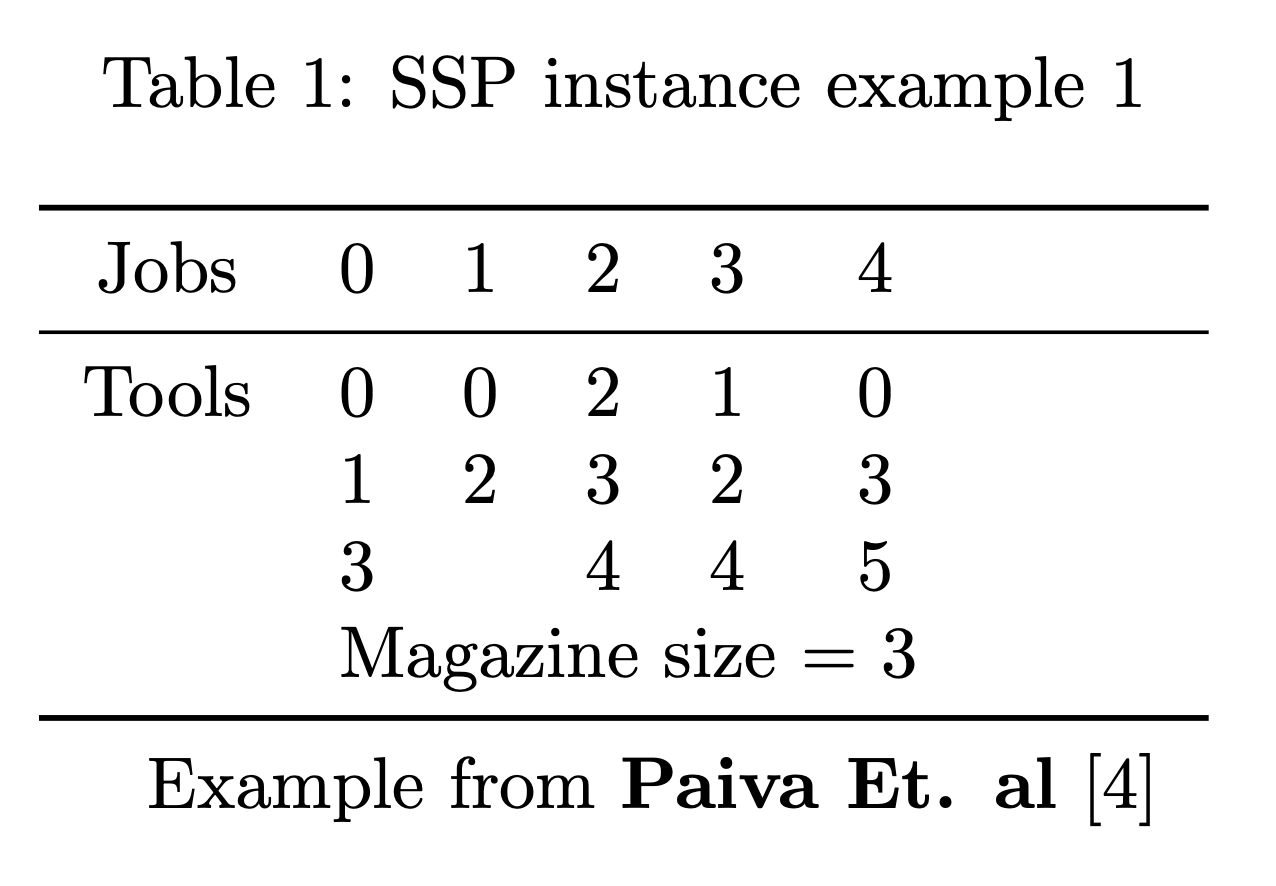
An instance can be modeled by way of a $M \times N$ binary matrix $A$, with $a_{ij} = 1$ if job j requires tool $i$, $0$ otherwise. ³. Thus, each column $j$ can be seen as $T_j$. As can be seen in table 1.

Example 1: binary matrix A

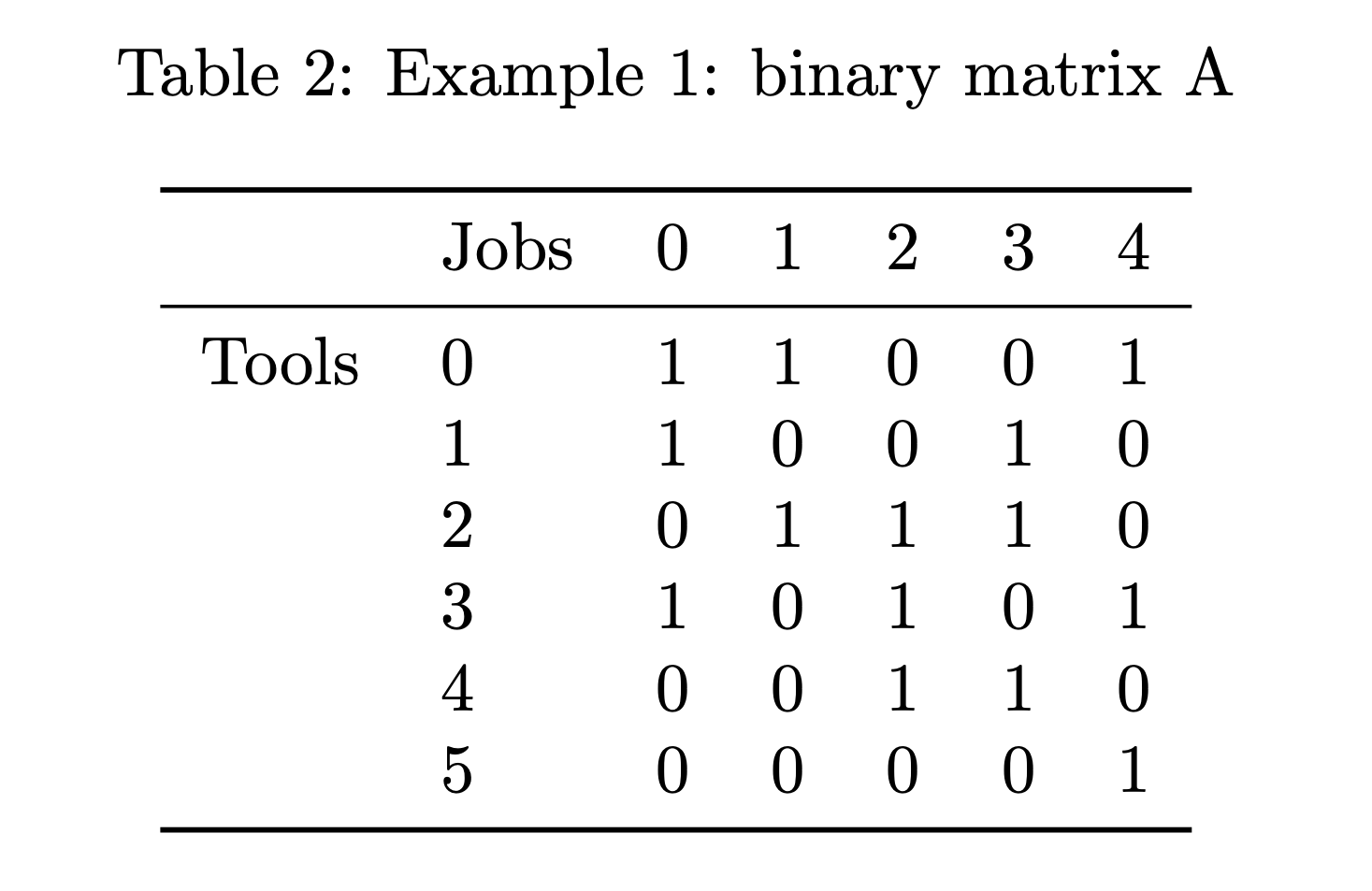
The solution to the problem is some sequence $\sigma$ which can be seen as a permutation of the set of jobs $J$. And a matrix $A^\ast$ , with $a^\ast_{ij} = 1$ if job $j$ requires or keeps tool $i$, $0$ otherwise. Alternatively, by permutating the columns of $A^\ast$ according to the sequence $\sigma$, the solution can be modeled as a $M \times N$ matrix P. This provides an intuitive way to interpret the state of the magazine at any time, as can be seen in figure 1³.

Figure 1Example 1: Permutation matrix P

Finally a tool setup can be considered as the insertion of a tool in the magazine. A tool switch is the combination of a tool setup and tool removal ³. The objective is to minimize the number of tool switches.

Properties

Tang and Denardo formally introduced the problem for the first time. They separated the problem in two subproblems:

• The sequencing problem (SP): Determine the order in which the jobs have to be executed. The sequencing problem is $\mathcal{NP}$ hard. As shown by ³
• The tooling problem (TP): Given the job sequence, determine which tools are needed at every position. Solvable in Polynomial time. As shown by ⁴

Although the Sequencing Problem is hard to solve, they demonstrated that the tooling problem is trivial. They introduced the "Keep Tool Needest Soonest" policy or "KTNS", which states the following:

• Tools are only inserted when they are needed.
• When tools need to be removed to accommodate new tools, remove the ones needed the least soon. i.e. “keep the tools needed soonest”

Applying this policy ensures that every job is able to use its required tools, additionally it uses the left over space in the magazine to accommodate tools that are required later. Beyond that, they proved that given a sequence $\sigma$ (SP), the optimal tool configuration (TP) can be found by using KTNS. This important fact enables us to model the problem as finding the optimal job sequence. Once a sequence is found the tool switches can be reduced by applying KTNS.

Moreover, by applying this policy the number of tool switches can easily be recognized each time a one turns into a zero in every row within $P$. Which is equivalent to replacing a tool by another one. ⁵.

Example 1: Permutation matrix with KTNS applied

Additionally Tang and Denaro proposed modeling the SSP as an instance of the Traveling Salesman Problem. They defined a weighted undirected graph $G= (V,E, lb)$, where the vertices V represent the set of jobs $J$, and the edges $\{i,j\} \in E$ represent job j following job i. Finally the weight of an edge $\{i,j\}$ is $lb(i,j) = max(|T_i \cup T_j| - C, 0)$, a lower bound for the amount of switches between job $i$ and $j$³.

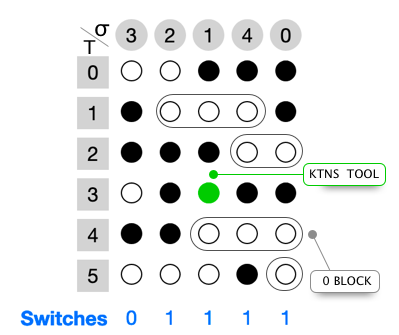
Crama Et al. ³ put forward the idea of recognizing $0/1$ blocks within the problem, as can be seen in figure 2. Interestingly the number of tool switches can only be reduced when we are able to eliminate a complete 0 block. This means we can reformulate the objective as reducing the amount of 0 blocks. Additionally, they reformulated KTNS as filling in the maximum amount of complete 0 blocks while respecting the constraints earlier mentioned.

Moreover they noticed that solving the problem as a TSP using the Lower bound proposed by Tang and Denaro does not work well when considering a sparse matrix. Due to the fact that a lot of tools can be added by KTNS. Ghiani Et al. ⁶ recognized a symmetry property within the problem. They stated and proved that thanks to KTNS the inverse of every job sequence has the same amount of tool switches. Which can be used to reduce the search space. Ultimately, a lot of attempts at the SSP have been made. Yet the difficulty of the SSP limits the ability of exact methods to be used on instances with more than $~25$ jobs ⁷. This illustrates the fact that a large portion of the research has put a focus on heuristic methods recently.

Methodology

Local Search

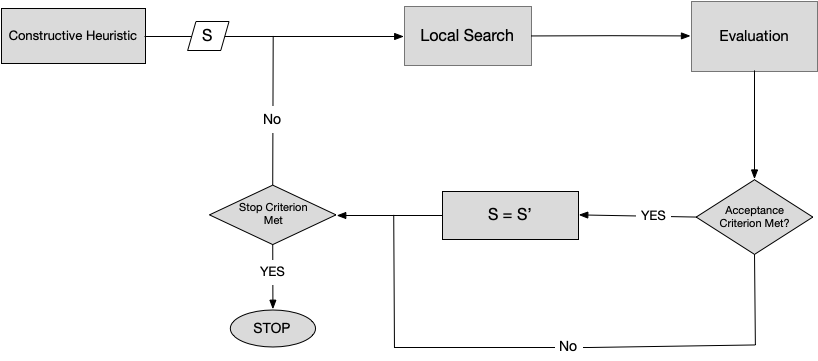
Local search is used to solve the SSP. Figure 3 illustrates the mechanism used. A solution to an instance of the SSP is represented by $S=\{\sigma, A^*\}$. The constructive by Paiva Et al. ⁸ is used.

Figure 3Local search method

Decoder

An indirect representation of the problem is used ⁵. When a solution is changed to a neighbor solution it is changed by permutating its job sequence. The full solution can be computed afterwards by performing $KTNS(\sigma)$ on the job sequence. Afterwards the solution is evaluated by counting the number of switches. We call the combination of these two steps the decoding of our solution. Algorithm 1 gives the algorithm used to perform KTNS. The developed algorithm does not use recursion as opposed to the algorithm proposed by Tang and Denardo ⁴.

KTNS

Ruin and Recreate

A new method is proposed for computing a candidate solution $S'$.

This method is based on Slack Induction by String Removals for Vehicle Routing Problems by ⁹. Ruin and recreate works by using one or more operators to destroy parts of a solution, and recreating it into a new candidate solution. The advantage of this method is that a large neighborhood can be explored. In our case the sequence $\sigma$ gets destroyed by removing certain jobs and recreated by inserting them again in a different place.

The method proposed here is called SMRI and uses 4 distinct phases: select, match, remove and insert. The method developed is visually illustrated on the next page step by step.

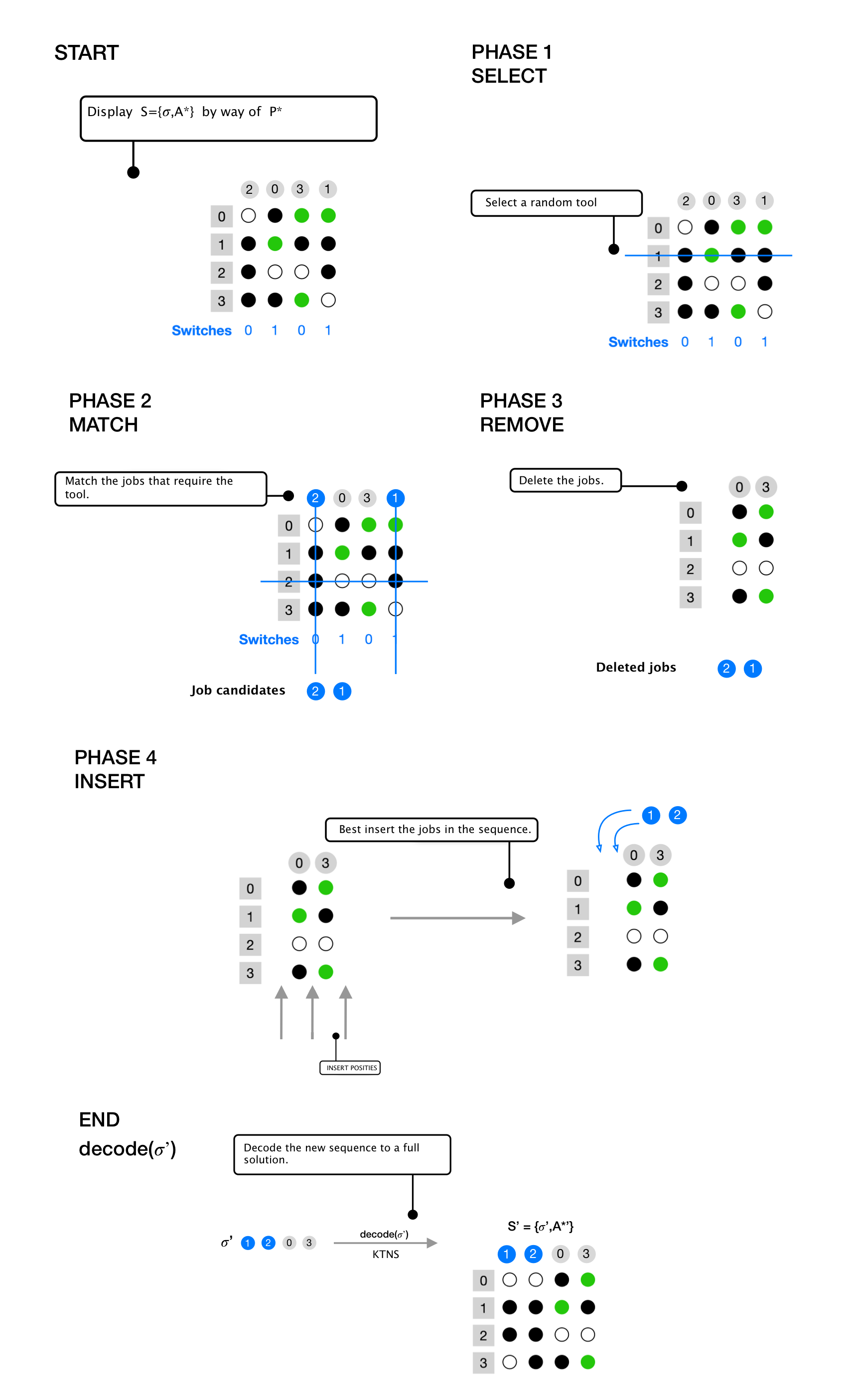
Meta Heuristic

Kirkpatrick Et. Al. ¹⁰ introduced Simulated Annealing, a meta heuristic based on the static model of Annealing. Annealing or annealing is a process used in the metal industry. It tries to get irregularities out of steel.

The systematic approach by Christiaens and Vanden Berghe ⁹ from Slack Induction by String Removals for Vehicle Routing Problems has been applied for the implementation of Simulated Annealing. Adjustments were made as needed for the application to this problem. The algortihm used is provided in Algorithm 2.

Simulated Annealing

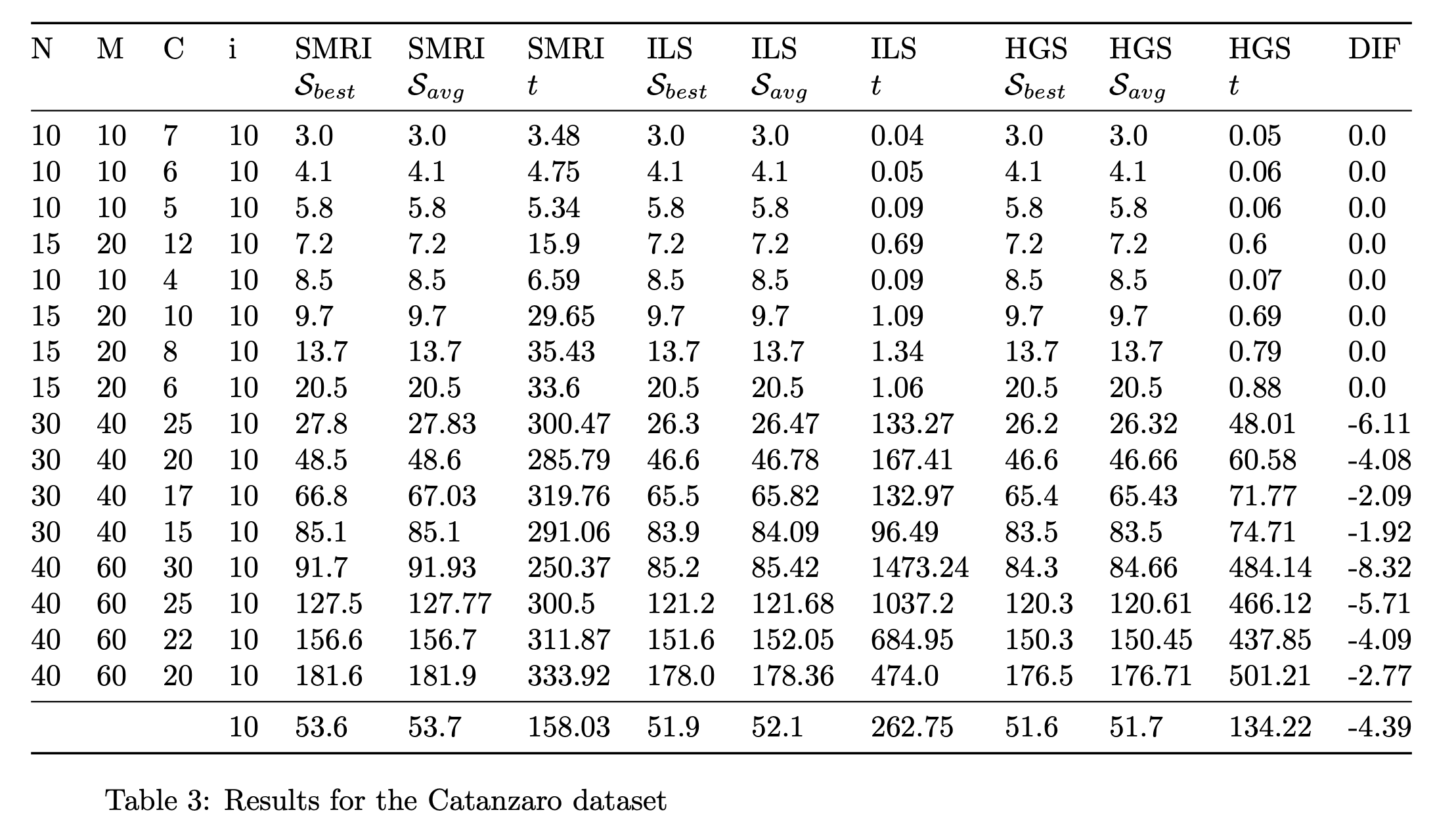
Results

Our new method is compared against the state of the art, using the dataset provided by Catanzaro Et al.. The results can be found in table 3 , last page. Our results (SMRI) are compared against the results of Paiva Et al.⁸ and Mecler Et al.⁵. The results where obtained from Mecler Et al.⁵. DIF stands for the percentage difference between the best solution and our solution, negative means ours is worse performing.

Results for the Catanzaro dataset

Conclusion

A new ruin and recreate method was introduced. As a ruin step, a tool is selected stochastically. Then all jobs requiring that tool are deleted. The logic here: these jobs are related. As a recreate step they are placed in the best place according to a greedy insert. Our methode did not exceed state of the art results. However, it was clear that the method proposed here has potential. It should therefore be further investigated.

References